Задача об оптимальном рационе питания
Выше рассмотрены простейшие модели динамики популяций с учетом конкуренции за пищевые ресурсы и влияния негативных факторов (например, эпидемий). Эти модели можно использовать для качественного анализа роста народонаселения. Конечно, рост численности населения сильно различается по разным странам и даже в развитых странах темпы роста неодинаковы. Например, в Дании, Швеции, Германии, Австрии этот показатель колеблется около нулевого значения. В таких странах, как Италия, Польша, Канада, США, рождаемость пока еще превышает смертность. Однако в целом в большинстве развитых стран ежегодный прирост населения составляет примерно 0,6% в год, тогда как в развивающихся странах – 2% в год.
В целом происходит стремительный рост населения на планете, что ставит насущную жизненную проблему управления природными ресурсами. При этом все отрасли управления ресурсами объединяет одна наука – экология и одна общая проблема – проблема оптимизации и, наконец, необходимость использовать одни и те же методы – взятие выборок, статистический анализ, математический анализ, логические процедуры, связанные с исследованием операций и анализом систем, применение вычислительной техники. Конечно, анализ и решение такой проблемы и даже какой-либо ее части представляет собой труднейшую задачу [30].
Начнем с рассмотрения простейшей задачи об оптимальном рационе, математическая модель которой допускает наглядную геометрическую интерпретацию. Пусть имеется п продуктов питания (хлеб, мясо, молоко, картофель и т.д.) и т
полезных веществ (жиры, белки, углеводы и т.п.). Обозначим через aij – содержание i-го вещества в единице j-го продукта, через bi, – потребность индивидуума в i-м веществе (скажем, в месяц) и через cj, – цену единицы j
-го продукта.
Обозначив потребление индивидуумом j-го продукта через хi, получаем задачу о выборе наиболее дешевого рациона питания (стоимости месячной продовольственной потребительской корзины):

при ограничениях

и

Такая задача называется задачей линейного программирования (в стандартной форме), общая теория которой рассмотрена, например, в [2].
Прежде чем исследовать задачу (11.1)–(11.3), заметим, что ее можно представить как задачу минимизации целевой функции f(x) =

f(х) > min, х Î Р .
(11.4)
Выясним, что представляет собой данный полиэдр Р на плоскости x1Ox2 в случае двух продуктов x1 и x2. Из неравенств (11.3) вытекает, что Р
расположен в первом квадранте, а каждое неравенство (11.2) геометрически определяет множество точек, лежащих по одну сторону от прямой

Для удобства введем линии уровня целевой функции, т. е. линии, на которых в плоскости х1Oх2 целевая функция
f(х)=с1x1+с2x2
(11.5)
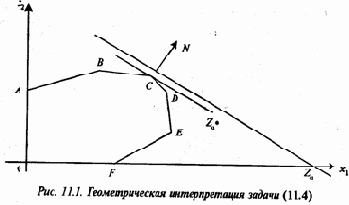
принимает постоянное значение, например, a, и обозначим ее Za. Очевидно, каждая линия уровня Za={(x1,x2):f(x)=a} является прямой; при этом gradf(x)=

перпендикулярным линии уровня и направленным (в данном случае) в сторону увеличения a. Таким образом, для нахождения оптимального решения нам следует перемещать линию уровня до касания с многоугольником OABCDE,
при этом оптимальная прямая Z

Из приведенной геометрической интерпретации вытекает, что минимум обязательно достигается на одной из вершин многоугольника, поэтому его можно было бы найти методом перебора, сравнивая между собой значения целевой функции во всех вершинах. Конечно, метод перебора в принципе годится и в случае п переменных, однако при больших значениях п он неэффективен.
Поэтому возникли и развиваются методы, позволяющие сформулировать более обозримые и эффективные критерии оптимальности. Начало им было положено работами акад. Л.В. Канторовича (1939 г.). Не углубляясь в суть этих методов, приведем пример одной многокритериальной модели.
В предыдущей задаче мы рассматривали одну целевую функцию. Однако на практике часто встречается ситуация, когда целенаправленная человеческая деятельность преследует сразу несколько целей. Такие задачи получили название многокритериальных. Методы их решения проиллюстрируем на только что рассмотренном примере составления оптимального рациона, несколько усложнив его.
Допустим, надо решить задачу об оптимальном рационе, максимизировав в нем первый продукт. Тогда наша математическая модель выглядит следующим образом:

Прежде чем приступить к решению, обсудим задачу, чтобы лучше понять ее специфику. Итак, забудем на время о первой целевой функции из (11.6). Тогда не составляет труда найти решение задачи:
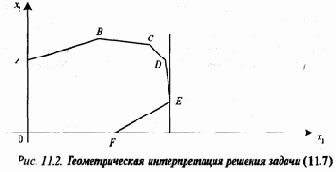
maxf2(x)=f2(E), xÎP (рис. 11.2). (11.7)
Однако значение первой целевой функции может быть значительно больше оптимального


1. Для реализации этого метода необходимо «взвесить» относительную важность каждого из критериев, т. е. выбрать из внемодельных соображений число e, 0 < e < 1, а затем построить одну целевую функцию

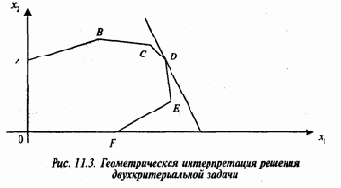
Если e=1. то в расчет принимается только первая целевая функция, а если e=0, то только вторая (рис. 11.1 и 11.2). Глубокое знание реальной проблемы и накопленный опыт могут позволить выбрать 0<e<1 так, чтобы, решив оптимизационную задачу с единственной целевой функцией, можно было бы получить удовлетворительное решение для исходной постановки задачи с двумя целевыми функциями (рис. 11.3).Встретив трудности при решении двухкритериальной задачи, можно заменить ее однокритериальной, решать которую мы умеем.